0. 背景
总所周知,即使是小朋友也知道
0.1+0.2 = 0.3肯定是正确的,但是在Java中,如果输入0.1+0.2 == 0.3,返回的却是false在Java中,如果你动手尝试输入
0.1+0.2,可以看到返回的值是0.30000000000000004,至于为什么会发生这样的事情,这便是后面要探讨的了——Java浮点数机制。
1. Java浮点数机制
通过查阅资料可以发现,现在很多主流的语言对浮点数的实现都是采用的IEEE 754,其中这些语言中也包含Java,要了解Java的浮点数机制,也就得了解IEEE 754是如何定义浮点数的
IEEE 浮点数标准是从逻辑上用三元组{S,E,M}来表示一个数 V 的,即 V=(-1)S×M×2^E
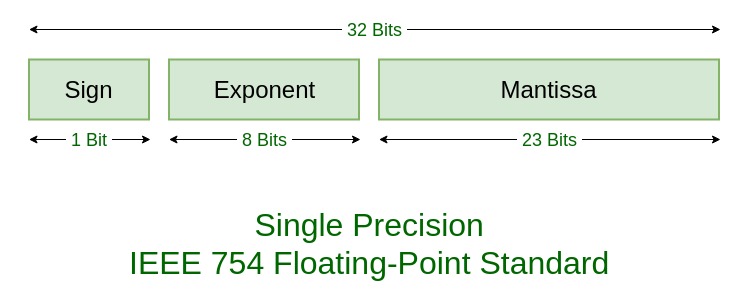
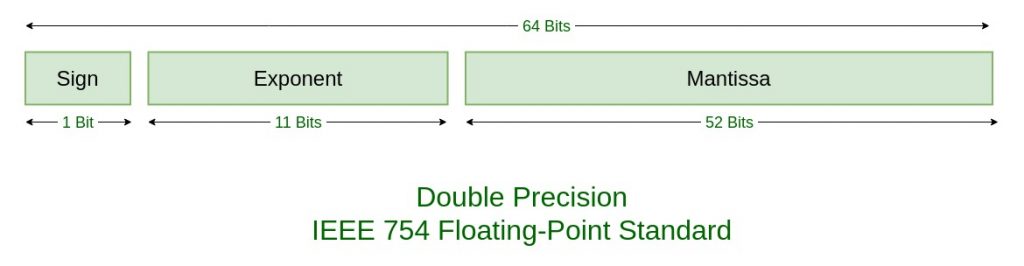
上图分别表示了不同精度的浮点数
其中: 符号位 s(Sign)决定数是正数(s=0)还是负数(s=1),而对于数值 0 的符号位解释则作为特殊情况处理。
有效数字位 M(Significand)是二进制小数,它的取值范围为 1~2-ε,或者为 0~1-ε。它也被称为尾数位(Mantissa)、系数位(Coefficient),甚至还被称作
小数。指数位 E(Exponent)是 2 的幂(可能是负数),它的作用是对浮点数加权。
| 类型(type) | 符号位(sign) | 指数位(biased exponent) | 有效数位(normalised mantisa) | 偏值(bias) |
|---|---|---|---|---|
| 单精度(Float) | 1(31st bit) | 8(30-23) | 23(22-0) | 127 |
| 双精度(Double | 1(63st bit) | 11(62-52) | 52(51-0) | 1023 |
下面用几个例子来做示范
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 原始值
85.125
// 转换成二进制形式
85 = 1010101
0.125 = 001
85.125 = 1010101.001
=1.010101001 x 2^6
// 正数
sign = 0
// 在单精度中的表现形式
// 指数位,因为需要用8位指数来表示正负两种情况,所以这里需要用6+偏值
biased exponent = 127+6 = 133
133 = 10000101
Normalised mantisa = 010101001 //后面将会自动补0到23位长度
// 所以在IEEE 754中该数的单精度的表示
0 10000101 01010100100000000000000
// 转换为十六进制
42AA4000
// 在双精度中的表现形式
biased exponent = 1023+6=1029
1029 = 10000000101
Normalised mantisa = 010101001 //后面将会自动补0到52位长度
// 所以在IEEE 754中该数的双精度的表示
0 10000000101 0101010010000000000000000000000000000000000000000000
// 转换为十六进制
4055480000000000
3. 为什么0.1+0.2 != 0.3
知道了在Java中的浮点数运行机制后,再来解决这个问题就很好办了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 第一步求出0.1的二进制形式
0.1 x 2 = 0.2 0
0.2 x 2 = 0.4 0
0.4 x 2 = 0.8 0
0.8 x 2 = 1.6 1
0.6 x 2 = 1.2 1
0.2 x 2 = 0.4 0
.....
// 所以最后计算出来0.1的二进制表现形式为一个无限循环小数
0.1 = 0.000110011001100.... x 2^0
// 使用IEEE754 来表示
1.10011 ... x 2^(-4)
0 1.1001100110011001100110 01111011
// 0.2 的最终表现形,指数位+1即可
0 1.1001100110011001100110 01111100
// 所以最后的0.3
0 1.0011001100110011001100 01111101
及
0 01111101 00110011001100110011001
// 再将次数转成二进制是就成了0.30000000000000004
所以0.1+0.2在Java中并不等于0.3
