概述
简单地说,k近邻算法采用测量不同特征值之间的距离方法进行分类。
k-近邻算法
- 优点:精度高、对异常值不敏感、无数据输入假定。
- 缺点:计算复杂度高、空间复杂度高。 适用数据范围:数值型和标称型。
工作原理:存在一个样本数据集合,也称作训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
算法简单实现
创建训练数据集&待分类数据
1
2
3
4
5
6
7
| # 导包
import numpy as np
import matplotlib.pyplot as plt
train_data = np.array([np.random.random()*10 for x in range(20)]).reshape(10,2) # 创建训练集
train_lable = np.array([0,1,1,1,0,0,1,1,0,1]) # 给每个向量一个标签
test_data = np.array([np.random.random()*10,np.random.random()*10]) # 待分类的目标值
|
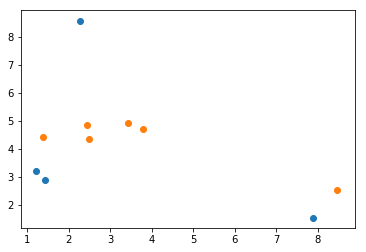
查看数据分布
![]()
计算分类点与数据集的距离
1
2
3
4
| K=3
len = np.array(np.sqrt(np.sum((train_data-test_data)**2,axis=1))) #axis=1 表示每次只计算一行
# 对值进行排序并取出下标的前K项
predict_lable = [train_lable[x] for x in len).argsort()[:K]]
|
取标签最后结果作为预测结果
1
2
| vote =Counter(predict_lable) # 对待分类值进行预测
vote.most_common(1)[0][0] # 输出预测结果
|
scikit-learn 中的KNN
导包&创建训练集
1
2
3
4
5
6
| import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier # 导包
train_data = np.array([np.random.random()*10 for x in range(20)]).reshape(10,2) # 创建训练集
train_lable = np.array([0,1,1,1,0,0,1,1,0,1]) # 给每个向量一个标签
|
创建KNN算法
1
| knn_clf = KNeighborsClassifier()
|
模型训练
1
2
3
4
5
| knn_clf.fit(train_data,train_label)
# out:
# KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
# metric_params=None, n_jobs=1, n_neighbors=2, p=2,
# weights='uniform')
|
分类预测
1
2
| test_data = np.array([np.random.random()*10,np.random.random()*10]) # 待分类的目标值
knn_clf.predict(test_data) # 使用训练类型进行预测
|
手动模型性能评估
加载sklearn中鸢尾花的数据
1
2
3
4
5
6
7
| import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris() # 加载数据
x = iris.data # 查看数据内容
y = iris.target # 数据对应的标签
|
数据下标重排
1
2
| np.random.seed(123) #输入随机种子
shuffle_indexes = np.random.permutation(len(x)) # 重排下标
|
数据集分割(训练集80%,测试集20%)
1
2
3
4
5
6
7
8
9
10
11
| test_radio = 0.2
train_len = int(0.2*len(shuffle_indexes))
train_index = shuffle_indexes[train_len:]
test_index = shuffle_indexes[:train_len]
# 训练集特征&标签
train_data = x[train_index]
train_lable = y[train_index]
# 测试集特征&标签
test_data = x[test_index]
test_label = y[test_index]
|
模型训练&数据预测
1
2
3
4
5
6
| from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
knn_clf.fit(train_data,train_lable)
predict_lable = knn_clf.predict(test_data)
|
精准度评估
1
| np.sum(test_label == predict_lable)/len(test_label)
|
scikit-learn中的模型性能评估
数据获取
1
2
3
4
5
6
7
8
| import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
iris = datasets.load_iris() # 加载数据
x = iris.data # 查看数据内容
y = iris.target # 数据对应的标签
|
数据分割
1
2
3
| from sklearn.model_selection import train_test_split
train_data,test_data,train_lable,test_lable = train_test_split(x,y,test_size=0.2,random_state=123)
|
模型训练&精准度计算
1
2
3
4
5
| # 模型训练
knn_clf = KNeighborsClassifier()
knn_clf.fit(train_data,train_lable)
# 精准度计算
knn_clf.score(test_data,test_lable)
|
超参数&模型参数
- 超参数:在模型运行前需要决定的参数
- 模型参数:算法过程中学习的参数
显然,KNN算法中没有模型参数
寻找最佳超参数
sklearn_KNeighborsClassifier API
class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights=’uniform’, algorithm=’auto’, leaf_size=30, p=2, metric=’minkowski’, metric_params=None, n_jobs=None, **kwargs)
从方法上可以看出一共有如下几个超参数
- n_neighbors:从待分类点最近K个值中进行判断,默认为5
- weights:距离权重,可选参数
- ‘uniform’:最近的K个点权重相同
- ‘distance’:最近的K个点中,近的点权重比远的点更高
- p :距离公式参数
- n_jobs:多少个job共同进行,
-1为使用全部进程
可以采用 for 循环来便利超参数来计算出最佳超参数
也可以使用网格搜索来计算
网格搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| param_grid=[
{
'weights':['uniform'],
'n_neighbors':[i for i in range(1,11)]
},
{
'weights':['distance'],
'n_neighbors':[i for i in range(1,11)],
'p':[i for i in range(1,6)]
}
]
from sklearn.neighbors import KNeighborsClassifier
knn_clf=KNeighborsClassifier()
from sklearn.model_selection import GridSearchCV
grid_search = GridSearchCV(knn_clf,param_grid,verbose=2)
%%time
grid_search.fit(train_data,train_lable) # 训练模型
grid_search.best_estimator_ # 返回最佳模型
grid_search.best_score_ # 返回精准度
|
归一化
最值归一化
![]()
均值方差归一化
![]()
![]()