1. 什么是特征缩放
在机器学习中特种缩放通常是指在数据预处理阶段,将不同量纲或量程的数据转换到同一量纲下或某个特定区间内。 例如,存在某一组特征范围:[0,100k] ,将其缩放至[0,1]之间,就是特征缩放
进行特征缩放的意义
- 改善算法性能:一些机器学习算法,特别是那些依赖于特征间距离的算法(如K-近邻、支持向量机等),对特征的尺度非常敏感。特征缩放确保了所有特征在同一尺度上,从而提高了这些算法的性能。举例说明:
特征x:[0,0.1] 特征y:[10k,100k],此时计算特征之间的欧式距离是很大的,但是如果都将缩放至[0,1]之间,特征之间的距离会大幅减少,可以有效增加算法性能,加速训练过程同理。
- 加速训练过程:某些基于梯度的优化算法(如梯度下降)在所有特征尺度相同时更容易找到最优解,从而加快训练过程。
- 增强模型解释性:当所有特征都在相同的尺度上时,可以更容易地解释模型,了解哪些特征对预测更有影响。
- 处理离群点和极端值:通过标准化,可以减小离群点和极端值对模型的影响。
2. 特征缩放的两大类方法
常用的特征缩放方法主要包括归一化(Normalization)和标准化(Standardization)。归一化通常将特征值转换到[0, 1]区间,而标准化则是将特征转化为具有零均值和单位方差的标准正态分布
2.1 归一化和标准化的对比
2.1.1 归一化 (Normalization)
- 计算方式: 将特征缩放到一个指定的范围,通常是[0, 1]。
- 适用场景: 当特征的量纲或数量级相差较大时,或当需要特征在一个固定范围内时。
- 优点:
- 将特征值约束在一个相同的范围内,有助于梯度下降等优化算法的收敛。
- 对于基于距离度量的算法如K-近邻、支持向量机等,归一化有助于量纲的消除。
- 缺点:
- 可能会丢失一些特征之间的相对差异信息。
- 受极端值的影响较大。
2.1.2 标准化 (Standardization)
- 计算方式: 将特征的均值移除并将其缩放到单位方差。
- 适用场景: 当特征分布不符合标准正态分布,或当算法假设输入特征是零均值和单位方差时。
- 优点:
- 通过消除均值和方差的影响,使得不同特征具有可比性,特别适合回归、逻辑回归、支持向量机等算法。
- 不受极端值的影响,更加稳定。
- 缺点:
- 不会将特征值限制在一个特定的范围内,对于某些需要固定范围输入的神经网络等算法,可能不太适合。
- 如果数据的分布远离正态分布,标准化可能效果不佳。
2.1.3 对比总结
- 使用归一化还是标准化取决于具体算法和数据的特性。
- 如果数据分布大致符合正态分布,标准化通常更有效。
- 如果特征的最小值和最大值已知并且重要,归一化可能更合适。
- 在不确定的情况下,可以尝试使用归一化和标准化,并使用交叉验证等方法选择效果更好的特征缩放方法。
2.2 归一化和标准化适用算法
归一化和标准化的对比表格,包括了各自适用的算法类型。
| 特性 | 归一化 (Normalization) | 标准化 (Standardization) |
|---|---|---|
| 计算方式 | 将特征缩放到[0, 1]范围内 | 移除均值并缩放到单位方差 |
| 适用算法 | K-近邻、神经网络、支持向量机等 | 线性回归、逻辑回归、支持向量机等 |
| 优点 | 量纲消除、有助于梯度下降等优化算法的收敛 | 不受极端值影响、特征可比性强 |
| 缺点 | 可能丢失相对差异、受极端值影响 | 不会将值限制在特定范围、非正态分布下效果可能不佳 |
注意:这些都是一般的指导原则,具体的选择可能需要根据具体数据和问题进行实验验证。
适用算法解释:
- 归一化:
- K-近邻: 基于距离的算法,需要特征在相同的量纲上。
- 神经网络: 有时需要输入特征在固定范围内以便更好地训练。
- 支持向量机: 对特征的量纲敏感。
- 标准化:
- 线性回归、逻辑回归: 假设特征是零均值和单位方差,标准化能满足这一假设。
- 支持向量机: 可以增强算法的稳定性和收敛性。
各类算法是否需要进行特征缩放
| 算法类型 | 是否需要缩放 | 实例算法 |
|---|---|---|
| 基于梯度下降的算法(Gradient Descent Based Algorithms) | 需要 | 逻辑回归、线性回归、神将网络等 |
| 基于距离的算法(Distance-Based Algorithms) | 需要 | K近邻、K-Means、SVM、PCA等 |
| 基于树的算法(Tree-Based Algorithms) | 不需要 | 决策树等 |
| 线性判别分析、朴素贝叶斯等算法 | 不需要 | 线性判别分析、朴素贝叶斯等 |
3. 常见特征缩放器功能&对数据的影响
- 数据来源:SKlearn中的加州住房数据
- x轴:街区收入中位数
- y轴:平均房屋占用率
3.1 原始数据
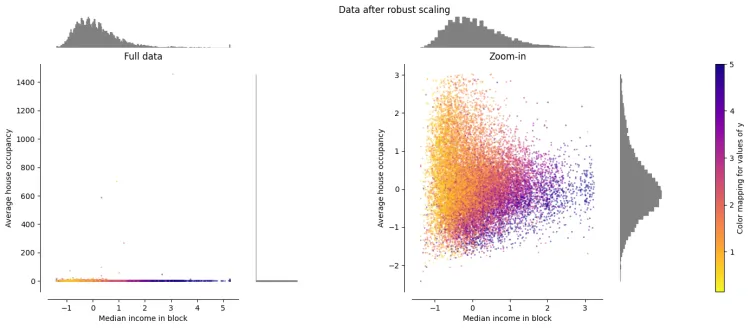
左侧图显示整个数据集,右侧图放大以显示没有边缘异常值的数据集。绝大多数样本都被压缩到特定范围,[0, 10] 代表收入中位数,[0, 6] 代表平均住房占用率 存在一些边际异常值(某些街区的平均入住人数超过 1200 人)需要注意
3.2 标准化 / Z值归一化(Standardization / Z-Score Normalization)
将数值缩放到0附近,且数据的分布变为均值为0,标准差为1的标准正态分布(先减去均值来对特征进行中心化 mean centering处理,再除以标准差进行缩放)。公式 \(Z = \frac{X - \mu}{\sigma}\)
- z 表示标准化后的值
- x 是原始特征值
- u 是该特征的均值(mean)
- _σ _是该特征的标准差(standard deviation)
转换后的数据:
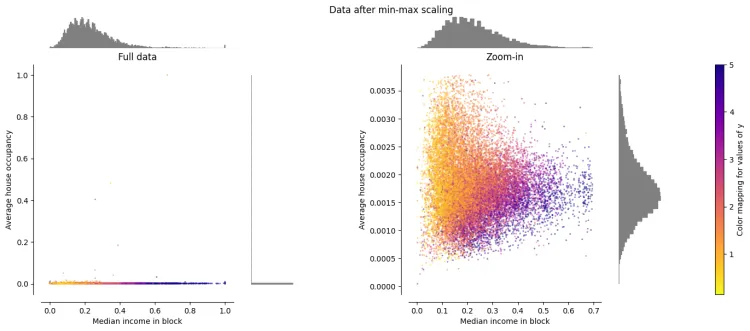
3.3 最大最小值归一化(Min-Max Normalization)
将数值范围缩放到指定范围区间里
\[x X_{scaled} = \frac{X - X_{min}}{X_{max} - X_{min}} \cdot (max - min) + min\]- X_scaled 是缩放后的值
- X 是原始特征值
- X_min 和 X_max 分别是该特征在整个数据集中的最小值和最大值
- max 和 min 是用户指定的缩放范围,默认通常是0和1
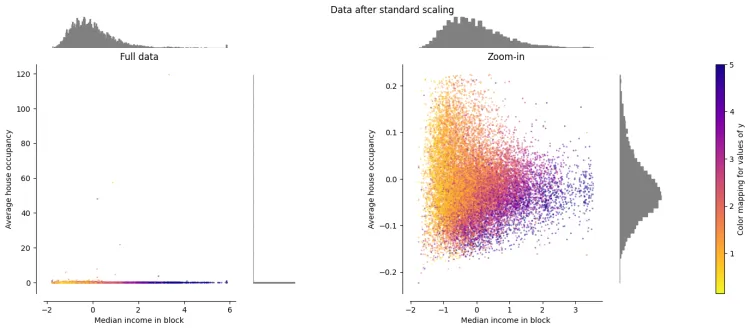
重新缩放数据集,使所有特征值都在 [0, 1] 范围内,如下右图所示。然而,这种缩放将所有内点压缩到转换后的平均房屋占用率的狭窄范围 [0, 0.005] 内 Z-Score Normalization和 Min-Max Normalization 对异常值的存在非常敏感
3.4 鲁棒标准化(Robust Standardization)
先减去中位数,再除以四分位间距(interquartile range),因为不涉及极值,因此在数据里有异常值的情况下表现比较稳健 \(X_{scaled} = \frac{X - Q_1}{Q_3 - Q_1}\)
- X_scaled 是缩放后的值
- X 是原始特征值
- Q_1 是该特征的第一四分位数(25%分位点)
- Q_3 是该特征的第三四分位数(75%分位点)
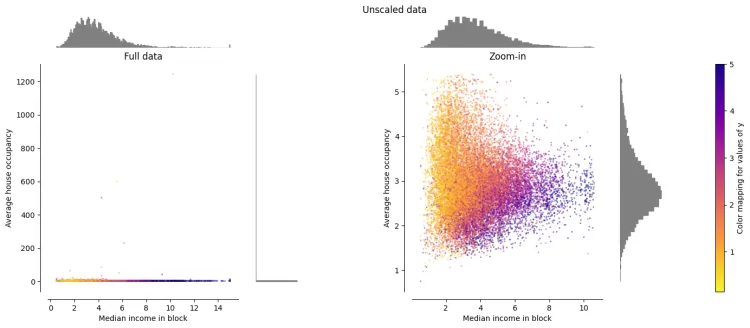
与之前的缩放器不同, Robust Standardization 的居中和缩放统计数据基于百分位数,因此不会受到少量非常大的边缘异常值的影响。因此,变换后的特征值的结果范围比之前的缩放器更大,更重要的是,近似相似; 对于这两个特征,大多数变换后的值都位于 [-2, 3] 范围内,如放大后的图像所示。图中。请注意,异常值本身仍然存在于转换后的数据中。如果需要单独的异常值剪切,则需要非线性变换
